ثنائي القطب RC

RC ثنائي القطب

RC شرح الجزء الخامس من درس الثنائي القطب

[KGVID]https://kezakoo.com/wp-content/uploads/2017/11/الثانية-باك-علوم-فيزيائية-_-الكهرباء-درس-ثنائي-القطب-RC-الجزء-الأخير-من-شرح-الدرس.mp4[/KGVID]

رابط المشاهدة على يوتيوب: https://youtu.be/Lbfcr3NLzyg

1. المكثف :

تعريف :  

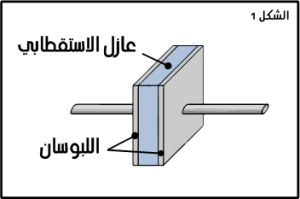
المكثف ثنائي قطب يتكون من موصلين متقابلين يسميان لبوسين Armatures يفصل بينهما عازل استقطابي.

يرمز للمكثف ب  :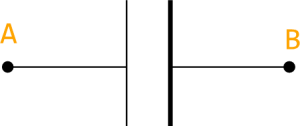 

شحن و تفريغ المكثف :

نشاط تجريبي 1 : ننجز التركيب الممثل أسفله (الشكل 2)

أ -  الشحن : نفتح قاطع التيار  K₁ ونغلق  K₂
بمتابعة مؤشر الفولطمتر ومؤشر الأمبيرمتر صف ما يحدث للتوتر بين مربطي المكثف و شدة التيار المار في الدارة - كيف تفسر شحن المكثف

ب -  التفريغ: نفتح قاطع التيار K₁ ثم نغلق  K₂
قارن منحى مرور التيار الكهربائي مع منحى مروره عند الشحن .
كيف تفسر تفريغ المكثف.

• الشحن : Charge

يشير الأمبيرمتر إلى مرور تيار كهربائي تتناقص شدته إلى أن ينعدم، يتزايد التوتر U_AB   إلى أن يصبح مساويا للقوة الكهرمحركة للمولد      U_AB = E  

تنتقل الإلكترونات من اللبوس   A   نحو اللبوس B  و تجد أمامها عازلا فتتركم عليه,  فيشحن اللبوس A  بشحنة q_A   موجبة  0˃q_A   بينما يشحن اللبوس B  بشحنة  q_B      سالبة    0˂q_B   بحيث :     q_A=- q_B 

نسمي شحنة المكثف q  الكمية الكهربائية التي يتوفرعليها أحد لبوسيه، حيث : 

عندما يشحن المكثف كليا (i = 0) يصبح U_AB=E

• التفريغ :  Décharge

نلاحظ مرور تيار عكس المنحى الذي مر فيه أثناء الشحن، حيث الإلكترونات المتراكمة على اللبوسB  تغادره نحو اللبوس  A  عبر الأمبيرمتر نقول إن المكثف ينفرغ  (se décharge) ي نتهي التفريغ (i = 0)   عندمل يصبح U_AB=0

• العلاقة بين الشحنة وشدة التيار i

نختار المنحى الموجب لشدة التيار، بحيث يدخل التيار من اللبوس A.

إذا مر التيار في المنحى الموجب المختار i˃0 وإذا مر عكس المنحى المختار يحسب سالبا i˂0

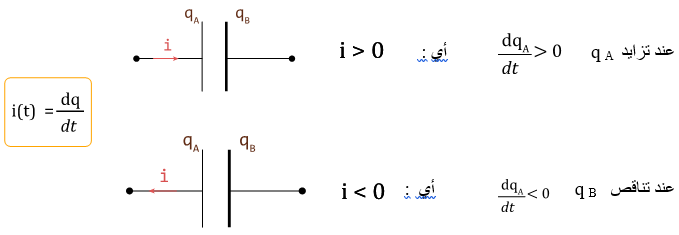
شدة التيار الكهربائي هي صبيب الشحنات الكهربائية أي كمية الكهرباء dq التي تمر في وحدة الزمن :

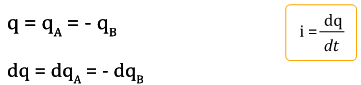
المكثف مُركبة تخزن كمية من الكهرباء وترجعها عند الحاجة.

العلاقة بين شحنة المكثف  q  والتوتر بين مربطيه U :   سعة المكثف (Capacité)

2. تجميع المكثفات :

 1.2. التركيب على التوالي :  

حسب قانون إضافيات التوتورات :

و بالتالي :   بحيث C : سعة المكثف المكافئ.

* بصفة عامة : التركيب على التوالي لمكثفات سعاتها  C_n, ………… C₂ , C₁  يكافئ مكثفا سعته C  بحيث :

فائدة التركيب على التوالي :
يمكن هذا التركيب من الحصول على سعه قيمتها اصغر مع تطبيق توتر عال قد لا يتحمله كل مكثف إذا استعمل لوحده.

2.2. التركيب على التوازي :

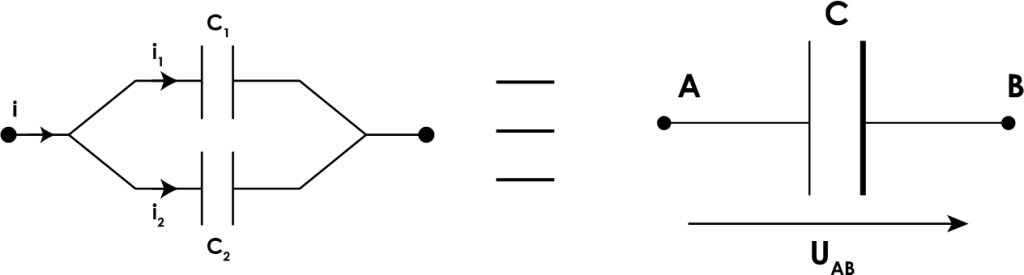
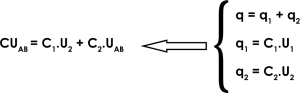
لدينا :  

وبالتالي :  
C  :   سعة المكتف المكافئ.

بصفة عامة :  التركيب على التوازي لمكثفات سعاتها  C_n, …….. C₂ ,C₁   يكافئ مكثفا سعته C   بحيث :
                                               C  = C₁ + C₂ + …………. + C_n

فائدة التركيب على التوازي :
يستعمل هذا التركيب لتضخيم السعة و تخزين شحنة كبيرة باستعمال مكثفات سعاتها صغيرة.

 3. استجابة ثنائي قطب  RC   لرتبة توتر :

تعاريف :  

ثنائي قطب RC  هو تجميع على التوالي لموصل أومي مقاومته R  و مكثف سعته C .

• رتبة توتر هي إشارة كهربائية تعرف كالتالي :

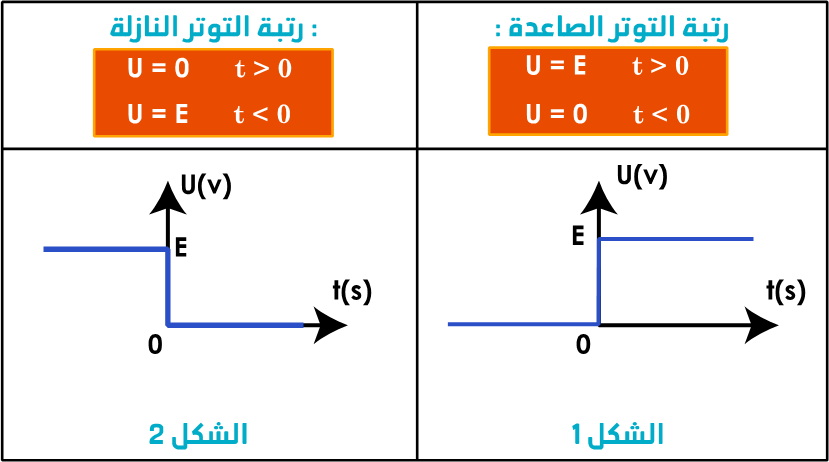
1.3. الدراسة التجربية :

1. نشاط تجريبي : شحن مكثف :  

بعد تفريغ المكثف , ننجز التركيب الكهربائي أسفله حيث                R = 1250Ω و   C = 0,4µF  ( الشكل 4)

نضبط مولد GBF ذا توتر مربعي توتره القصوي E = 6V وتردده  f = 200Hz.

نغلق قاطع التيار K في الموضع 1 ونعاين بواسطة كاشف التذبذب التوتر UC (t)  بين مربطي المكثف بدلالة الزمن.

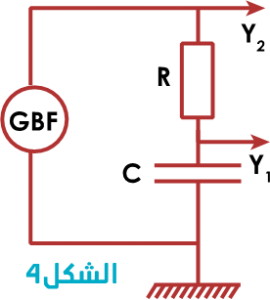
1 - ما هو المنحنى الذي نشاهده على المدخل Y1 وما هو المنحنى الذي نشاهده على المدخل Y2 ؟

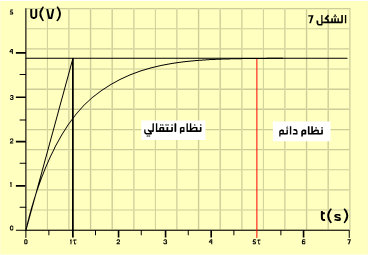
2 - نعتبر حالة توتر ذي رتبة صاعدة. يبرز منحنى تغيرات UC(t) وجود نظامين:
نظام انتقالي   : يتغير خلاله التوتر     Uc(t)
نظام دائم: يصل خلاله التوتر إلى قيمة حدية ثابتة.
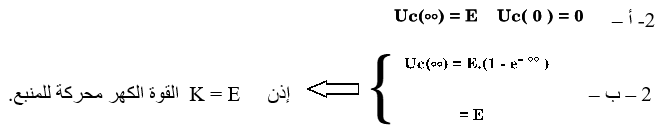
أ – عين Uc(t) و Uc(οο) عندما تؤول t إلى ما نهاية.
ب – نعبر عن المنحنى Uc(t) بدلالة الزمن , بالدالة حيث k و τ ثابتتان , حدد الثابتة k . ماذا تمثل ؟
نعطي = 0 e- οο

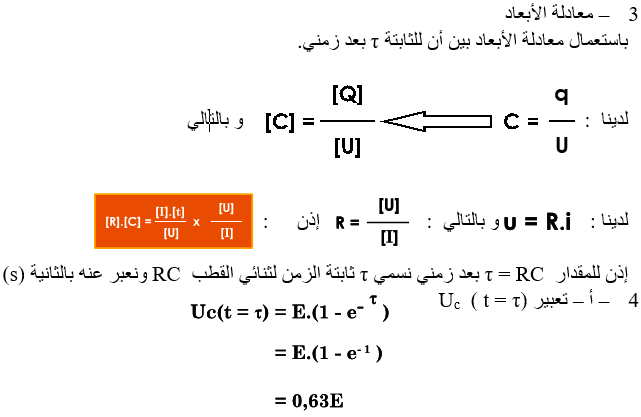
3 – تسمى  ثابتة الزمن لثنائي القطب RC وتبين الدراسة النظرية أن : RC =
باستعمال معادلة الأبعاد بين أن  عبارة عن زمن.

4 – نعتبر الدالة الممثلة للمنحنى (Uc(t
أ – عبر عن  بدلالة E  التي تم التعرف عليها في السؤال (2 – ب)
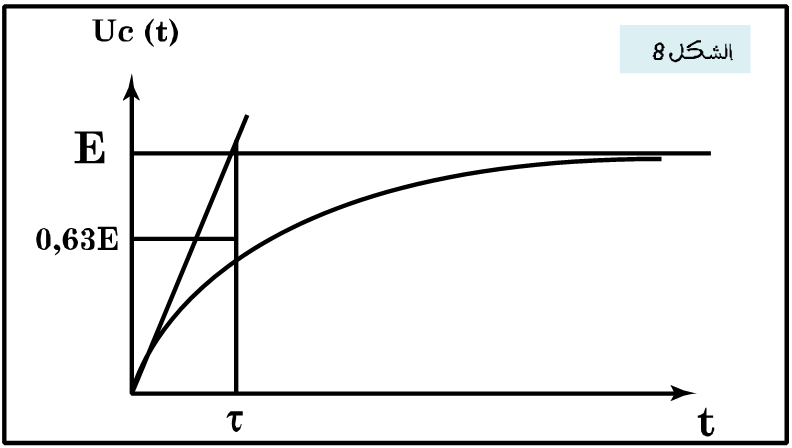
ب – استنتج مبيانيا قيمة
د – يمكن أن نحددبطريقة مبيانية ثانية حيث تمثل أفصول نقطة تقاطع المماس لمنحنى (Uc(t   عند t = 0  من المنحنى (1) حدد باستعمال هذه الطريقة.

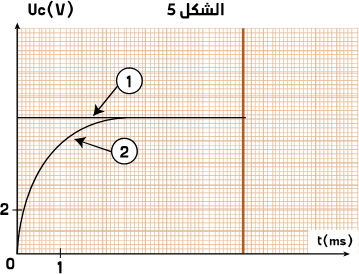
الأجوبة :

1 – المنحنى الذي نشاهده على المدخل Y1  هو رقم 2، والمنحنى الذي نشاهده على المدخل Y2  هو رقم 1.

5– ب – نستنتج مبيانيا قيمة

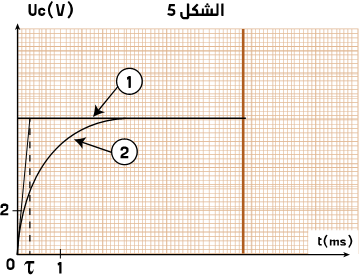
الأفصول الذي يوافق الأرتوب  0,63.E ت ع :

4 – ج - RC = 1250 × 0 ,4.10-6 = 0,5.10-3 s = 0,5 ms
4 – د – تحديد ثابتة الزمن مبيانيا :
يقطع مماس المنحنى     (Uc = f(t عند اللحظة    t = 0  المقارب   Uc = E

في اللحظة    t  = 

2. تفريغ المكثف :  

نؤرجع قاطع التيار عند الموضع 2.
يفرغ المكثف في القاومة  R  و يتناقص التوتر Uc  بين مربطيه.

تحديد ثابتة الزمن مبيانيا :
المماس للمنحنى (Uc = f(t .

النظامان الإنتقالي و الدائم:
أ – نظام انتقالي :  Régime transitoire
يتزايد أو يتناقص خلاله التوتر Uc   و نحصل عليه عندما تكون   t˂5τ
ب – النظام الدائم :  Régime permanent
نحصل عليه عندما يكون t˃5  و يبقى خلاله التوتر Uc  ثابتا (Uc = E)  عند شحن المكثف (Uc = 0)  عند تفريغ المكثف.

2.3 . الدراسة النظرية :

1. شحن مكثف :

أ – المعادلة التفاضلية :   

ملحوضة :  

باعتبار 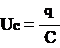  المعادلة التفاضلية التي تحققها الشحنة q   :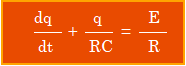  

ب – حل المعادلة التفاضلية :   

يكتب حل المعادلة التفاضلية :  
A  و  B   و α  ثوابت.

• تحديد B  و  α :  

تحديد A   باستعمال الشروط البدئية :

عند اللحظة  t = 0  فإن  Uc = 0   (لم يكن المكثف مشحونا).

نعوض في العلاقة التفاضلية فنحصل على :    يعني A = - B = - E

إذن   نضع = RC

تعبير التوتر بين مربطي مكثف :

ملحوظة :

لدينا :  q = C.Uc   و منه :

الشحنة الكهربائية :  

شدة التيار i 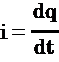   و منه :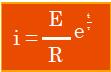  

الطريقة الحسابية لتحديد ثابتة الزمن  :  

لدينا :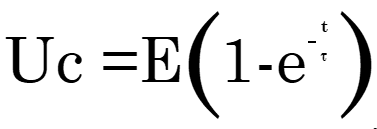 

عند t =  فإن الأرتوب :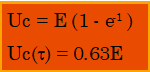  

2. تفريغ المكثف :

أ – المعادلة التفاضلية :  

نؤرجح قاطع التيار إلى الموضع 2.

               

 

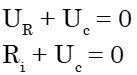
و بتالي : 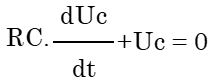    ومنه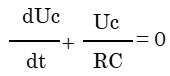 

ملحوظة :  

باعتبار  نجد المعادلة  التفاضلية التي تحققها الشحنة q :  

ب – حل المعادلة التفاضلية :

يكتب حل المعادلة التفاضلية على الشكل التالي :   Uc = Ae^-αt + B

-   تحديد الثوابث A  و B   و α :  

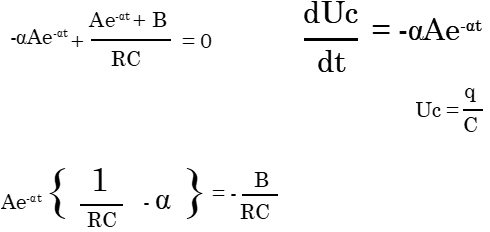
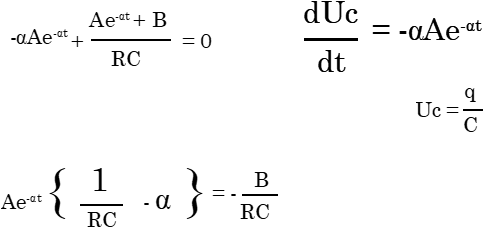
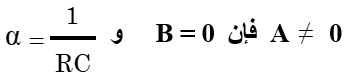
تحديد الثوابث عند الشروط البدئية :

عند t = 0   فإن Uc = E   و منه A = E   إذن :

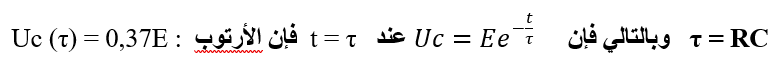
ملحوظة :  

لدينا q = C.Uc  ومنه :

- الشحنة الكهربائية :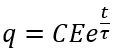   

شدة التيار i   :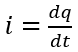

و منه :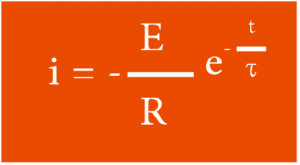  

 4. الطاقة المخزونة في مكثف :  

يمكن المكثف من تخزين طاقة كهربائية قصد استعمالها عند الحاجة.

تعبير الطاقة المخزونة في المكثف :  

أو : 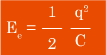 مع   :      q = C.U

 

المكثف

تعريف المكثف