La géométrie est une branche en mathématiques, et durant les années précédentes nous avons découvert des théorèmes permettant de calculer la longueur des côtés notamment dans un triangle, à titre d’exemple : Pythagore, Thalès…Mais, ces théorèmes permettent seulement d’établir des relations entre un côté et un autre. Les mathématiciens ont introduit un concept consistant à lier la mesure des côtés avec la mesure des angles dans un triangle rectangle nommé le calcule trigonométrie.$\\$
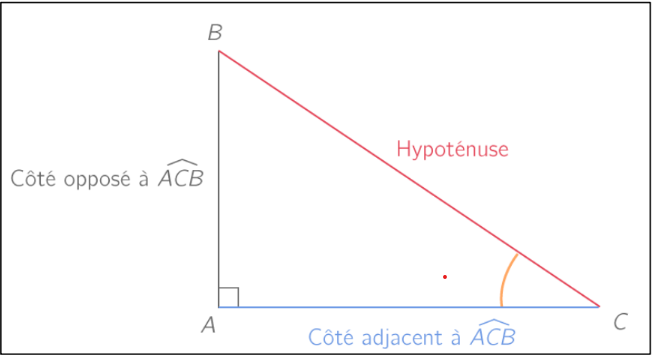
Nous définissons le sinus, le cosinus et tangent par :$\\$
$\begin{aligned}\sin (\widehat{ACB}) &=\frac{\text { côté opposé à } \widehat{ACB}}{\text { Hypoténuse }} \\[0.2cm] \cos (\widehat{ACB}) &=\frac{\text { côté adjacent à } \widehat{ACB}}{\text { Hypoténuse }} \\[0.2cm] \tan (\widehat{ACB}) &=\frac{\text { côté opposé à } \widehat{ACB}}{\text { côté adjacent à } \widehat{ACB}}\end{aligned}$
Rappel
Notions de base
تعريف
Le cercle trigonométrique est une
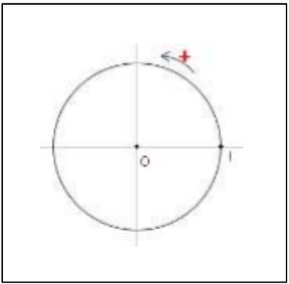 illustration permettant de mettre en évidence les angles en radian et les trois fonctions trigonométriques : Cosinus, Sinus et tangent. Pratiquement, c’est un cercle :
illustration permettant de mettre en évidence les angles en radian et les trois fonctions trigonométriques : Cosinus, Sinus et tangent. Pratiquement, c’est un cercle :
- De centre $O(0;0)$ l’origine du plan
- De Rayon$R=1$
- Orienté positivement
- $I$ un point pour entamer le calcul.
Remarque
Soit $\boldsymbol{M}(\boldsymbol{x}, \boldsymbol{y})$ un point de cercle corresponde à l'angle $\boldsymbol{t}=(\overrightarrow{\boldsymbol{O I}}, \overrightarrow{\boldsymbol{OM}})$, alors
- $\quad x=\cos (t)$
- $\quad y=\sin (t)$
- $ \quad \frac{y}{x}=\tan (t)$ Si $x \neq 0$
Résultats
1. $\forall x \in$ IR, $-1 \leq \cos (x) \leq 1$ et $-1 \leq \sin (x) \leq 1\\[0.2cm]$
2. $\forall x \in$ IR, $\cos ^{2}(x)+\sin ^{2}(x)=1$ Car le rayon est $1$ et l'origine de cercle c'est $O\\[0.2cm]$
3 . $ \forall x \in I R, \sin (x+2 \pi)=\sin (x)$ et $\cos (x+2 \pi)=\cos (x)\\[0.2cm]$
4. $\forall x \in I R \backslash\left\{\frac{\pi}{2}+k \pi\right. $ avec $\left.k \in Z\right\}, \tan (x)=\frac{\sin (x)}{\cos (x)} \\[0.2cm]$
5. Les deux fonctions : Sinus et tangent sont impairs. $\\[0.2cm]$
6. La fonction Cosinus est pair.
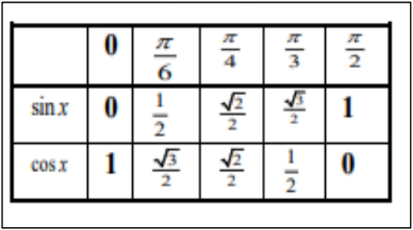
Le tableau des angles usuelles
Les équations trigonométriques
Equation $ \cos (x)=a $
Considérons l'équation $\cos (x)=a$ avec $a \in I R: $
1. Si $a \in]-\infty ;-1[\mathrm{U}] 1 ;+\infty[$ alors l'équation n'admet pas de solution $\\[0.2cm]$
2. Si $a=1$ alors les solutions de l'équation sont : $ 2 \pi k$ avec $k \in Z\\[0.2cm]$
3. Si $a=-1$ alors les solutions de l'équation sont: $ \pi+2 \pi k$ avec $k \in Z\\[0.2cm]$
4. Si $-1<a<1$ alors $\exists \alpha \in] 0, \pi[$ vérifiant $\cos (\alpha)=a$ alors l'ensemble des solutions d'équation : $S=\{\alpha+2 k \pi, k \in Z\} \cup\{-\alpha+2 k \pi, k \in Z\}\\[0.2cm]$ Généralement, les solutions de l'équation $\cos (u(x))=\cos (v(x)) $, avec $u$ et $v$ deux fonctions, sont : $\left\{\begin{array}{l}u(x)=v(x)+2 k \pi, k \in Z \\[0.2cm] u(x)=-v(x)+2 k \pi, k \in Z\end{array} \text{ ou }\right. $
Equation $ \sin (x)=a $
Considérons l'équation $\sin (x)=a$ avec $a \in I R: \\[0.2cm]$
1. Si $a \in]-\infty ;-1[\cup] 1 ;+\infty[$ alors l'équation n'admet pas de solution $\\[0.2cm]$
2. Si $a=1$ alors les solutions de l'équation sont $: \frac{\pi}{2}+2 \pi k$ avec $k \in Z\\[0.2cm]$
3. Si $a=-1$ alors les solutions de l'équation sont $:-\frac{\pi}{2}+2 \pi k$ avec $k \in Z\\[0.2cm]$
4. Si $-1<a<1$ alors $\exists \alpha \in]-\frac{\pi}{2}, \frac{\pi}{2}[$ vérifiant $\sin (\alpha)=a$ alors l'ensemble des solutions d'équation : $\\[0.2cm]S=\{\pi-\alpha+2 k \pi, k \in Z\} \cup$ $\{\alpha+2 k \pi, k \in Z\}\\[0.2cm]$ Généralement, les solutions de l'équation $\sin (u(x))=\sin (v(x)) $, avec $u$ et $v$ deux fonctions, sont: $\left\{\begin{array}{c}u(x)=v(x)+2 k \pi, k \in Z \\[0.2cm] u(x)=\pi-v(x)+2 k \pi, k \in Z\end{array}\right.$ Ou
Equation $ \tan (x)=a $
Considérons l'équation $\tan (x)=a(E)$ avec $a \in I R$, alors il existe un et un seul nombre appartient à l'intervalle $]-\frac{\pi}{2}, \frac{\pi}{2}[$ vérifiant $: \tan (\alpha)=a$ et l'ensemble des solutions de $(E) $ est $:\{\alpha+k \pi, k \in Z\} . \\[0.2cm]$ Généralement, les solutions de l'équation $\tan (u(x))=\tan (v(x)) $, $\\[0.2cm]$ avec $u(x) \neq \frac{\pi}{2}+k \pi \text { et } v(x) \neq \frac{\pi}{2}+k \pi \\ \text { pour tout } x \in I R \text { et } k \in Z\\[0.2cm]$ Donc les solutions seront l'ensemble des réels $x: u(x)=v(x)+k \pi, k \in I R$
Les inéquations trigonométriques
La résolution des inéquations liée fortement à la partie précédente, car la première étape pour aboutir à l’ensemble des solutions dans un intervalle est la résolution de l’équation correspondent. Nous traiterons des exemples concrètes afin d’assimiler chaque type d’inéquation :
Inéquation Cosinus
Exemple
Résoudre l’inéquation suivante dans $ [-\pi, \pi] $ : $\cos (x) \geq \frac{1}{2}$
Corrigé exemple
Etape 1 : la résolution de l’équation correspondante, autrement $ \cos (x)=\frac{1}{2} $ : $\cos (x)=\frac{1}{2} \Leftrightarrow \cos (x)=\cos \left(\frac{\pi}{3}\right) \Leftrightarrow\left[\begin{array}{l}\frac{\pi}{3}+2 k \pi, k \in Z \\-\frac{\pi}{3}+2 k \pi, k \in Z\end{array}\right.\\[0.2cm]$ Puisque nous travaillons dans $[-\pi, \pi]$ alors les deux points admissibles sont : $\frac{\pi}{3}$ et $-\frac{\pi}{3}\\[0.2cm]$
Etape 2 : il s'agit de déterminer l'ensemble des solutions de l'inéquation en se basant sur les deux points $: \frac{\pi}{3}$ et $-\frac{\pi}{3}$, puisque l'équation est en cosinus donc nous cherchons les abscisses dont la valeur est plus que $\frac{1}{2}$ mais en restant toujours dans l'intervalle $[-\pi, \pi] \\[0.2cm]$ Pour expliciter les solutions il faut revenir au cercle trigonométrique :
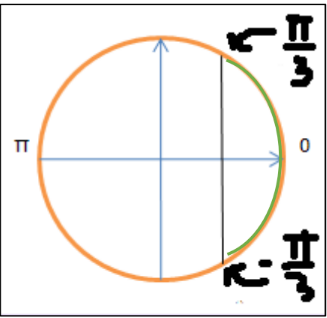
Donc l'ensemble des solutions est l'arc en vert :$S=\left[-\frac{\pi}{3}, \frac{\pi}{3}\right]$
Inéquation sinus
Exemple
Résoudre l’inéquation suivante dans $[0,2 \pi]: $ $\sin (x) \geq \frac{1}{2}$
Corrigé exemple
Etape 1: la résolution de l'équation correspondante, donc $\sin (x)=\frac{1}{2}\\[0.2cm]$ $\sin (x)=\frac{1}{2} \Leftrightarrow \sin (x)=\sin \left(\frac{\pi}{6}\right) \Leftrightarrow\left\{\begin{array}{l}\frac{\pi}{6}+2 k \pi, k \in Z \\[0.2cm]\frac{5 \pi}{6}+2 k \pi, k \in Z\end{array}\right.\\[0.2cm]$
Puisque nous travaillons dans $[0,2 \pi] $ alors les deux points admissibles sont $: \frac{\pi}{6}$ et $\frac{5 \pi}{6}\\[0.3cm]$
Etape 2 : il s'agit de déterminer l'ensemble des solutions de l'inéquation en se basant sur les deux points $: \frac{\pi}{6}$ et $\frac{5 \pi}{6},$
puisque l'équation est en sinus donc nous cherchons les ordonnées dont la valeur est plus que $\frac{1}{2}$ mais en restant toujours dans l'intervalle $ [0,2 \pi]\\[0.2cm]$ Pour expliciter les solutions il faut revenir au cercle trigonométrique
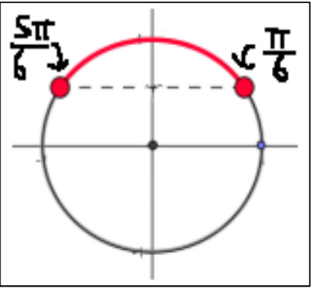
Donc l’ensembles des solutions est l’arc en rouge : $ S=\left[\frac{\pi}{6}, \frac{5 \pi}{6}\right] $
Inéquation de tangent
Exemple
Résoudre l’inéquation suivante dans $ [0,2 \pi]: \tan (x)-1 \geq 0 $
Corrigé exemple
Etape 1 : la résolution de l’équation correspondante, $\\[0.2cm]$ donc $\tan (x)-1=0 \Leftrightarrow \tan (x)=1\\[0.2cm]$ On a $\tan \left(\frac{\pi}{4}\right)=1\\[0.2cm]$ alors $tan (x)=1 \Leftrightarrow \tan (x)=\tan \left(\frac{\pi}{4}\right) \Leftrightarrow x=\frac{\pi}{4}+k \pi, k \in I R\\[0.2cm]$ Puisque nous travaillons dans $[0,2 \pi]$ alors les deux points admissibles sont : $\frac{\pi}{4}$ et $\frac{5 \pi}{4}\\[0.3cm]$
Etape 2 : il s’agit de déterminer l’ensemble des solutions de l’inéquation en se basant sur les deux points : $ \frac{\pi}{4}$ et $\frac{5 \pi}{4} \\[0.2cm]$ puisque l’équation est en tangent donc nous cherchons les points $M(x,y)$ sur le cercle trigonométrique dont la valeur de point d’intersection entre la droite tangente à l’origine et la droite de vecteur directeur $ \overrightarrow{O M}$ est supérieur ou égale à $1$ mais en restant toujours dans l’intervalle $ [0,2 \pi].\\[0.2cm]$ Pour expliciter les solutions il faut revenir au cercle trigonométrique
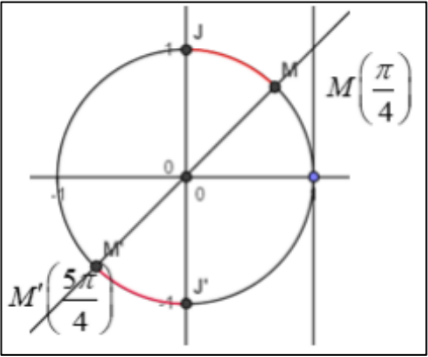
Donc l’ensembles des solutions est les deux arcs en rouge : $ S=\left[\frac{\pi}{4}, \frac{\pi}{2}\left[\cup \left[\frac{5 \pi}{4}, \frac{3 \pi}{2}[\right.\right.\right. $
Formules Trigonométriques
Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo

- Fiches de cours illimitées
- Une vidéo gratuite par leçon
- 2 exercices gratuits par leçon
- Un test gratuit par leçon