Rappel :
Produit scalaire de deux vecteurs :
- L’expression du produit scalaire en utilisant la projection orthogonale :
Soient $\mathrm{A}$ et $\mathrm{B}$ et $\mathrm{C}$ trois points dans le plan et $\mathrm{H}$ la projection orthogonale du point $\mathrm{C}$ sur la
droite (AB).Alors le produit scalaire de $\overrightarrow{A B \text { et }} \overrightarrow{A C}$ est le nombre réel $\overrightarrow{A B} \cdot \overrightarrow{A C}$ tel que :
- $$\overrightarrow{A B} \cdot \overrightarrow{A C}=A B \times A H \operatorname{si} \overrightarrow{A B} \text { et } \overrightarrow{A H} \text { ont le même sens. }$$
- $$\overrightarrow{A B} \cdot \overrightarrow{A C}=-A B \times A H \text { și } \overrightarrow{A B} \text { et } \overrightarrow{A H} \text { n'ont pas le même sens. }$$
- $$\text { Si } \overrightarrow{A B}=0(A=B) \text { ou } \overrightarrow{A C}=0(A=C) \text { alors } \overrightarrow{A B} \cdot \overrightarrow{A C}=0$$
- La formule trigonométrique du produit scalaire :
Soient $\overrightarrow{A B}$ et $\overrightarrow{A C}$ deux vecteurs du plan alors:
$$\overrightarrow{A B} \cdot \overrightarrow{A C}=\|A B\| \times\|A C\| \times \cos (\overline {\overrightarrow{A B}, \overrightarrow{A C}})=A B \times A C \times \cos (\overline{\overrightarrow{A B}, \overrightarrow{A C}})$$
Remarque :
$$\text { Le nombre réel positif } \sqrt{\overrightarrow{A B} \cdot \overrightarrow{A B}} \text { est appelé la norme du vecteur } \overrightarrow{A B} \text { et on note }\|\overrightarrow{A B}\|=A B \text { . }$$
خاصية
$$\begin{array}{l} (\vec{u}+\vec{v}) \cdot \vec{w}=\vec{u} . \vec{w}+\vec{v} \cdot \vec{w} \\ \vec{w} \cdot(\vec{u}+\vec{v})=\vec{w} \cdot \vec{u}+\vec{w} \cdot \vec{v} \\ \vec{u} .(\alpha \vec{v})=(\alpha \vec{u}) \cdot \vec{v}=\alpha(\vec{u} \cdot \vec{v}) \end{array}$$ $$\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{u}$$ $$\vec{v}^{2}=\vec{v} \cdot \vec{v} \geq 0$$ $$\vec{v} \cdot \vec{v}=0 \Leftrightarrow \vec{v}=0$$ $$\vec{u} \perp \vec{w} \Leftrightarrow \vec{u} \cdot \vec{w}=0$$ Remarque : $$\begin{aligned} &\text { Dans toute la suite de ce cours, on considère le plan muni à un repère orthonormé directe }\\ &(O, \vec{\imath}, \vec{j}) \end{aligned} $$ [kezakoo section ="propriete"] Soient $\vec{u}(x, y)=x \vec{\imath}+y \vec{\jmath}$ et $\vec{v}\left(x^{\prime}, y^{\prime}\right)=x^{\prime} \vec{\imath}+y^{\prime} \vec{\jmath}$ deux vecteurs du plan $(P)$.On a :
برهان
$$A B=\|\overrightarrow{A B}\|=\sqrt{\overrightarrow{A B} \cdot \overrightarrow{A B}}=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}$$ Exemple : On donne $\vec{u}=\vec{\imath}-2 \vec{\jmath}$ et $\vec{v}=-4 \vec{\imath}+2 \vec{\jmath}$ et $A(0,3)$ et $B(2,-1)$ $$\vec{u} . \vec{v}=1 \times(-4)+(-2) \times 2=-4-4=-8$$ $$\begin{array}{l} \|\vec{u}\|=\sqrt{1^{2}+(-2)^{2}}=\sqrt{5} \\ \|\vec{v}\|=\sqrt{(-4)^{2}+2^{2}}=\sqrt{20} \end{array}$$ $$A B=\sqrt{(2-0)^{2}+(-1-3)^{2}}=\sqrt{4+16}=\sqrt{20}$$ On a :
برهان
$$\begin{array}{l} \left\{\begin{array}{c} \vec{u} . \vec{v}=\|\vec{u}\| \times\|\vec{v}\| \times \cos \theta \\ \vec{u} \cdot \vec{v}=x x^{\prime}+y y^{\prime} \end{array}\right. \\ \Rightarrow\left\{\begin{array}{c} \cos \theta=\frac{\vec{u} \cdot \vec{v}}{\|\vec{u}\| \times\|\vec{v}\|} \\ \vec{u} . \vec{v}=x x^{\prime}+y y^{\prime} \end{array}\right. \end{array}$$ Donc: $$\cos \theta=\frac{x x^{\prime}+y y^{\prime}}{\sqrt{x^{2}+y^{2}} \times \sqrt{x^{\prime 2}+y^{\prime 2}}}$$ $$\begin{array}{l} (\overline{\vec{v}, \vec{w}}) \equiv(\overline{\vec{v}, \vec{u}})+(\overline{\vec{u}, \vec{w}})[2 \pi] \equiv-\theta+\frac{\pi}{2}[2 \pi] \\ \vec{v} \cdot \vec{w}=\|\vec{v}\| \times\|\vec{w}\| \times \cos \left(-\theta+\frac{\pi}{2}\right)=\|\vec{v}\| \times\|\vec{u}\| \times \sin \theta \mid \\ \Rightarrow \sin \theta=\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\| \times\|\vec{u}\|} \end{array}$$ Et on a $\vec{w}(-y, x)$ Donc: $$\sin \theta=\frac{x y^{\prime}-x^{\prime} y}{\sqrt{x^{2}+y^{2}} \times \sqrt{x^{\prime 2}+y^{\prime 2}}}$$ Ou autrement : $$\sin \theta=\frac{\operatorname{det}(\vec{u} . \vec{v})}{\sqrt{x^{2}+y^{2}} \times \sqrt{x^{\prime 2}+y^{\prime 2}}}$$ Exemple : Soient les trois points $A(5,0), B(2,1)$ et $C(6,3)$ : a- Calculons $\cos (\overline{\overrightarrow{A B}, \overrightarrow{A C}})$ : On a : $$\begin{array}{r} \cos (\overline{\ overrightarrow {A B}, \overrightarrow{A C}})=\frac{\overrightarrow{A B} \cdot \overrightarrow{A C}}{\|A B\| \times\|A C\|}=\frac{(-3 \vec{\imath}+\vec{\jmath})(\vec{\imath}+3 \vec{\jmath})}{A B \times A C} \\ A B=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}=\sqrt{(-3)^{2}+1^{2}}=\sqrt{10} \\ A C=\sqrt{\left(x_{C}-x_{A}\right)^{2}+\left(y_{C}-y_{A}\right)^{2}}=\sqrt{1^{2}+3^{2}}=\sqrt{10} \end{array}$$ Donc: $$\cos (\overline {\overrightarrow{A B}, \overrightarrow{A C}})=\frac{-3+3}{10}=0$$ b- Calculons $\sin (\overline {\overrightarrow{A B}, \overrightarrow{A C}})$ : On a : $$\sin (\overline{\overrightarrow{A B}, \overrightarrow{A C}})=\frac{(-3) \times 3-1 \times 1}{10}=-\frac{10}{10}=-1$$ Donc: $$(\overline{\overrightarrow{A B}, \overrightarrow{A C}}) \equiv-\frac{\pi}{2}[2 \pi]$$ Pour continuer cette fiche de cours, Inscris-toi gratuitement sur Kezakoo
Base orthonormée directe – Repère orthonormé directe :
L’expression analytique du produit scalaire et la norme d’un vecteur dans un repère orthonormé directe :
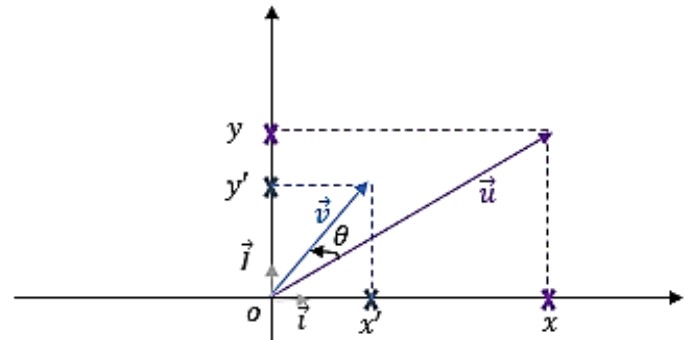
Formules de cos (u,v) et sin (u,v) :
[kezakoo section ="propriete"] Soient $\vec{u}(x, y)=x \vec{\imath}+y \vec{\jmath}$ et $\vec{v}\left(x^{\prime}, y^{\prime}\right)=x^{\prime} \vec{\imath}+y^{\prime} \vec{\jmath}$ deux vecteurs non nuls dans le plan et $(\overline{\vec{u}, \vec{v}}) \equiv \theta[2 \pi]$
L’air d’un triangle et d’un parallélogramme :

![]() Signaler une erreur
Signaler une erreur