-
-
Maths
Continuite
2ème année bac Sciences Math A Mathématiques Limites et Continuité fiche de cours
Continuité d'une fonction en un point
تعريف
Soit $$f$$ une fonction numérique définie sur un intervalle ouvert $$I$$ et $$x_0$$ un élément de l'intervalle $I$ On dit que la fonction $$f$$ est continue au point $$x_0$$ si:
$$\lim\limits_{x \to x_0} f(x) =f(x_0)$$
En d'autres termes:
$$(\forall \epsilon >0)(\exists \alpha >0) ~~ |x-x_0|<\alpha \Rightarrow ~~ |f(x)-f(x_0)|<\epsilon$$
مثال
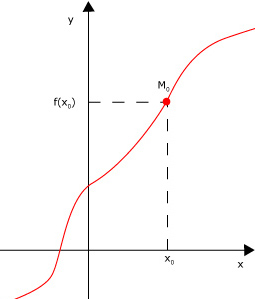
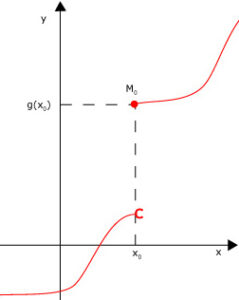
La fonction $$f$$ représentée ci-dessous est continue en $$x_0$$. La fonction $$g$$ est discontinue en $$x_0$$. Autrement dit, on voit graphiquement qu'une fonction est continue en un point $$x_0$$ si la courbe passe par le point $$M_0$$ $$(x_0 ; f(x_0))$$ sans coupure. Sinon, la fonction est discontinue en ce point.
مثال
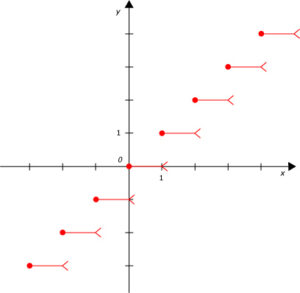
La fonction partie entière de $$x$$, notée $$E$$, est discontinue en tout point entier. $$E(x)$$ est le plus grand entier relatif inférieur ou égal à $$x$$. Par exemple, $$E(\pi) = 3$$ ; $$E(-\pi) = -4$$ ; $$E(\sqrt{2}) = 1$$ ; $$E(5) = 5$$ et $$E(-8) = -8$$. Voici la représentation graphique de cette fonction :
Continuité à gauche, continuité à droite
تعريف
Soit $$f$$ une fonction définie sur l'intervalle $$[x_0; x_0+r[$$ où $$r>0$$
- On dit que la fonction $$f$$ est continue à droite en $$x_0$$ si:
$$\lim\limits_{x \to x_0^+} f(x)=f(x_0)$$
Soit $$f$$ une fonction définie sur l'intervalle $$[x_0-r; x_0[$$ où $$r>0$$
- On dit que la fonction $$f$$ est continue à gauche en $$x_0$$ si:
$$\lim\limits_{x \to x_0^-} f(x)=f(x_0)$$
Continuité en un point
Une fonction numérique $$f$$ est continue en $$x_0$$ si, et seulement si elle est continue à droite et à gauche au point $$x_0$$. En d'autres termes:
$$f$$ est continue au point $$x_0$$ $$\Leftrightarrow \lim\limits_{x \to x_0^-} f(x)= \lim\limits_{x \to x_0^+} f(x) =f(x_0)$$
Prolongement par continuité en un point
تعريف
Soit $$f$$ une fonction numérique non définie en un point $$x_0$$ et admettant une limite finie $$l$$ en $$x_0$$:
$$ \lim\limits_{x \to x_0} f(x)=l / l \in \mathbb{R}$$
Alors la fonction $$g$$ définie par:
$$\left\{\begin{array}{lcl} g(x)=f(x) x \ne x_0 \\ g(x_0)=l \end{array} \right.$$
est continue en $$x_0$$, et est appelée le prolongement par continuité de $$f$$ au point $$x_0$$
Continuité d'une fonction sur un intervalle
لمواصلة هذا الملخص، قم بالتسجيل بالمجان في كيزاكو
- ملخصات الدروس غير محدودة
- فيديو مجاني في كل درس
- تمرين مصحح مجاني
- اختبار تفاعلي
Signaler une erreur